本文共 3353 字,大约阅读时间需要 11 分钟。
一家被称为硅谷最神秘的独角兽公司将要上市了。
9月30日晚间,大数据公司Palantir正式登陆纽交所。上市首日股价一度涨超34%,随后便跌破其开盘价10美元。截至周五发稿时,盘后股价上涨0.80%至10.08美元。相较于上市首日超200亿美元市值,目前市值仅为44.10亿美元。

(图源:雪球)
上半年,Palantir身处的大数据分析赛道一直备受投资者关注。Splunk和datadog等数据分析公司的二季度股价都迎来了一波连续暴涨,分别上涨了57%和141%。但近期大盘的调整却让市场对科技股的买入热情有所降温。结合招股书来看,这一时间段上市的Palantir,未来能否复刻今年诸多数据分析公司的表现呢?
估值缩水、直接上市,Palantir神秘背景将揭开面纱
早在上市前,这家公司就已经被外界频繁讨论。Palantir诞生于硅谷,作为一家成立18年的公司,在长时间跨度里经历了估值的剧烈变动。
2015年,外媒报道其估值约200亿美元,是硅谷估值最高的公司之一,而在这之前估值一直忽高忽低。而本月外媒再次报道,Palantir提交的文件显示估值降至105亿美元,较5年前缩水一半。
估值波动的背后,是投资者对于其成长性的摇摆。公司17年从未获得盈利,市场逐渐降低了信心,但成立至今却又累计获得共80亿美元融资。
如此充满争议,主要源自于Palantir富有神秘色彩的业务。公司专门从事数据收集和分析,其目标客户是G端。自身的技术主要应用于国防与安全领域,为政府提供服务,2011年之后才陆续有少数商业客户接入,这与其他大部分公司专注B端和C端的方向截然相反。
值得注意的是,Palantir是继Spotify与Slack之后,第三个选择直接上市的科技独角兽。这意味着公司本身有着足够知名度,或者资金雄厚无需立刻借外部筹集更多资金。无论是哪一种,都至少反映其内部对Palantir公司本身充满着信心。对于这样一家神秘公司的发展,我们也许能够从其招股书中窥知一二。
业务版图逐季扩张,G端成二季度营收“主力军”
和最初成立时的经营路径不同,Palantir发展至今其实已形成to B和to G相结合的经营模式。
招股书显示,今年第二季度营收为2.52亿美元,同比增长42.9%,低于第一季度的同比增速56.8%。
短期来看,未来几个季度的营收数据有望维持二季度的好成绩。因为第三季度和第四季度迎来政府机构和公司陆续签订合作协议,因此一定程度上对整体营收起到提振的作用。
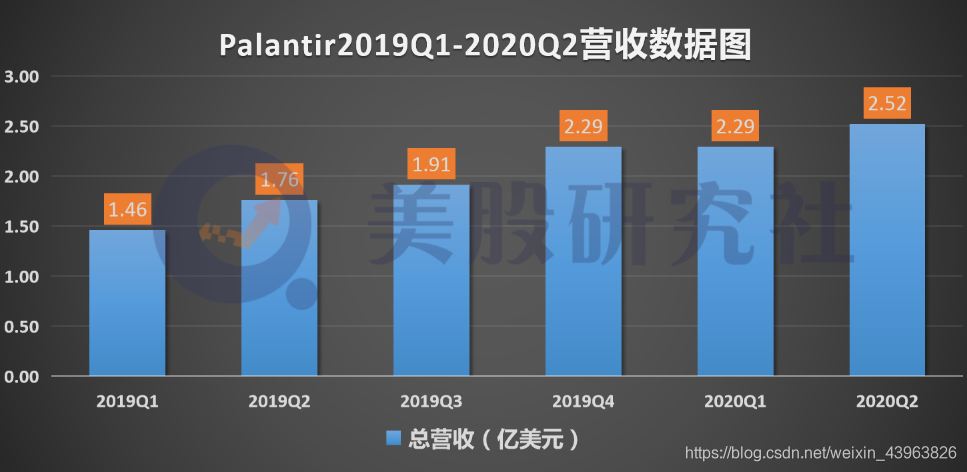
从整体趋势上看,公司营收呈现逐季上行趋势,这意味着其经营规模在进一步扩大,已建立了一定的市场地位。
据统计,Palantir平均年度营收增速为41%,高于老牌数据分析公司Splunk的36%,但相比初创公司Datadog来说仍有差距。datadog近几年迎来高速增长,19年营收较18年扩大83.3%。
其中G端是公司上半年的核心收入来源。招股书显示,今年上半年来源政府的收入为2.58亿美元,同比增长76%,占比为53.6%。

由于大环境的影响,政府机构为帮助在特殊时期能够合理高效地调配和使用资源,因此增加了大量数据分析的合作订单。但是,由于本季度转化了大量潜在客户达成合作协议,因此公司G端营收增速放缓的风险较高,第三四季度旺季过后可能增速将进一步回落。
不过,市面上大多数云服务企业都是为B端和C端客户服务,因此Palantir在G端途径上面对的竞争压力并不大。
最需要关注的是,亚马逊、微软等科技巨头的最新动作。
亚马逊和微软都与政府机构建立过云服务合作,不排除亚马逊、微软、谷歌等科技巨头利用自身技术优势,与政府机构达成新的合作协议以抢占Palantir的市场份额。若科技巨头未来在其云平台上推出类似的功能,对于Palantir拓展G端业务是一个极大的威胁。
拓展B端市场挖增长点,高支出成数据分析企业共同痛点
实际上,多年之前G端一直是公司的主要收入来源。但2011年通过与摩根投行合作,开始迈入金融领域,此后公司来源于商业客户的收入占比便在不断增加。
招股书显示,2018年商业收入为3.40亿美元,超过政府收入2.55亿美元;而2019年商业收入为3.97亿美元,同比增长17%,超过政府收入的3.45亿美元。

但是无论从上半年还是从财年情况看,商业收入都远低于政府收入的同比增速。Palantir一直表示将业务逐步拓展商业,但从目前的情况看显然不乐观。
有别于政府机构,短期内企业受经济不佳影响必然会减少对于数据分析服务的需求,这在一定程度上会抑制公司在B端的营收增长。
目前公司的数据分析平台都运行在亚马逊AWS、微软Azure等公共云服务上,而这样方式此前迎来亚马逊和微软内部员工和外部团体的抗议。早在2018年,就有450名AWS员工联名签署信函,要求CEO贝佐斯从平台上移除Palantir。虽然CEO没有同意,但面临的压力在未来仍可能加剧
除了上述的问题,摆在Palantir面前的还有B端客户稀少的困境。招股书显示,今年上半年公司共有125名客户。显然,单拎出B端客户来说这个数量更少。
截至19年末,Splunk已经积累了约1.9万家客户,而datadog在最新季度已经拥有1.31万名订阅用户。
相比之下,公司业务的客户集中度极高,有限数量的客户对业务的影响很大,如果现有客户没有续订与公司的合作协议,会对业务增长造成巨大的冲击。

虽然上市后可以通过积极拓展新用户来逐步摆脱这一困境,但对公司控制成本的能力又是一大考验。第二季度公司的营销费用和研发费用分别为1.03和0.87亿美元,分别同比减少7.3%和增加10.3%。
公司在招股书中表示,将在软件平台方面继续投资,而且近期还扩大了直销队伍,预计还将继续扩大这支队伍。短期来看,这些费用依旧会是制约盈利能力的重要一环。
多个季度的费用一直处于高位,使得公司一直未取得盈利。招股书显示,公司最新季度经营亏损0.99亿美元,净亏损为1.10亿美元。而2019年整年,经营亏损和净亏损分别为5.76亿和5.80亿美元。
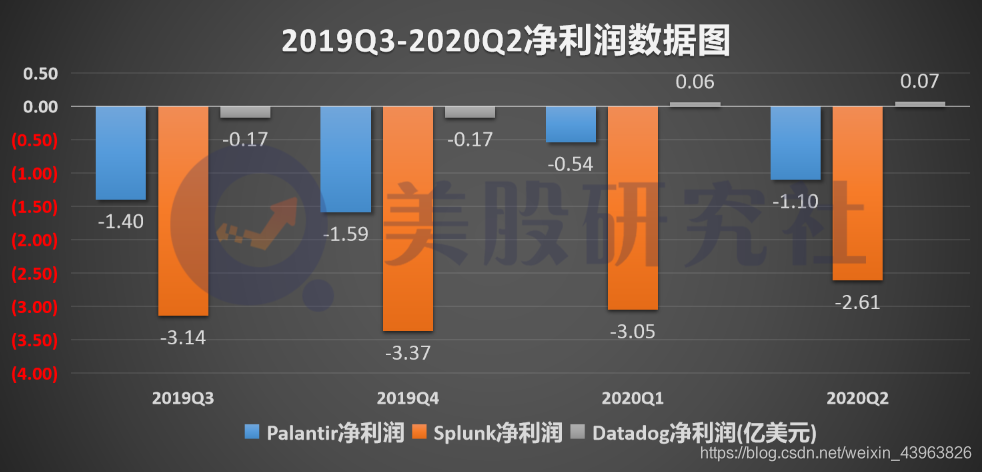
高昂的费用同样制约着其他数据分析公司的盈利能力。Splunk第二季度净亏损为2.39亿美元,同比增长176%;而datadog虽然在最新季度摆脱亏损,但净利润也极低。
对于任何一家公司,目前欠佳的盈利状况短期内很难有扭亏的可能。这也使得外界对于palantir能否支撑起科技公司的高估值打上了问号。
定制化服务贯穿垂直领域,Palantir能否再现数据分析赛道辉煌?
在数据分析赛道上亏损的公司远远不止Palantir、Splunk和Datadog这三家公司。上市后,任何一家科技公司若要享受资本市场的青睐,更应该向市场证明其拥有巨大的潜在发展空间,Palantir自然也是如此。

不同于其他两家公司,Palantir一直致力于将技术应用拓宽到不同行业中的各种垂直领域,将数据分析贯穿到更多的场景,这或许是Palantir的长期价值所在。
据统计,Palantir业务自2008年以来已覆盖至36个行业,最新涉及的行业有食物及原材料零售、交通、矿业电力等等。更早地贯穿到各个垂直领域,在多个领域内能够率先确立竞争优势。
而且,Palantir诞生于美国,但积极扩张全球业务,这无疑给公司的长期发展前景加分。在2019年,40%的收入来自美国客户,而60%都来自国外客户。
不过,受抑于本身的商业模式,让公司的产品短期内很难在多个行业中的大量企业中铺开。
包括Splunk和Datadog在内大多数企业更多向客户推出通用解决方案,订阅即用的形式适应更多的客户使用。
Palantir却与之相反,其解决方案并不通用,往往需要根据客户的差异化需求进行定制化,定制化后的成果不存在普适性。这也就意味着,Palantir的定制多为半成品搭配数据专业人员,客户将高度依赖专业人员。但是,这种方式更能够挖掘出具体一家企业甚至整个行业更多价值,长期看可能会成为更多企业客户的选择。
数据分析市场处在高速发展中,对于任何一家公司都有机会。Palantir的商业模式具有独立性,很难被复制,未来的潜力或许更大。
本文来源:美股研究社,转载请注明版权